转载自：惠店长

线性回归模型属于经典的统计学模型，该模型的应用场景是根据已知的变量（自变量）来预测某个连续的数值变量（因变量）。

例如，根据大众点评中的推广费，来预测店铺曝光量的情况。

一元线性回归模型。

该模型中只含有一个自变量和一个因变量，该模型的数学公式可以表示为：y=a+bx+e。

下图中的直线称为回归直线，a称为回归常数，它是回归直线的截距，b也称为回归系数，它是回归直线的斜率，e是一切随机因素影响的总和，称为随机误差项。

以下将讨论根据店铺的历史数据，来预测此店铺在一天中花费多少推广费，将带来多少曝光量。

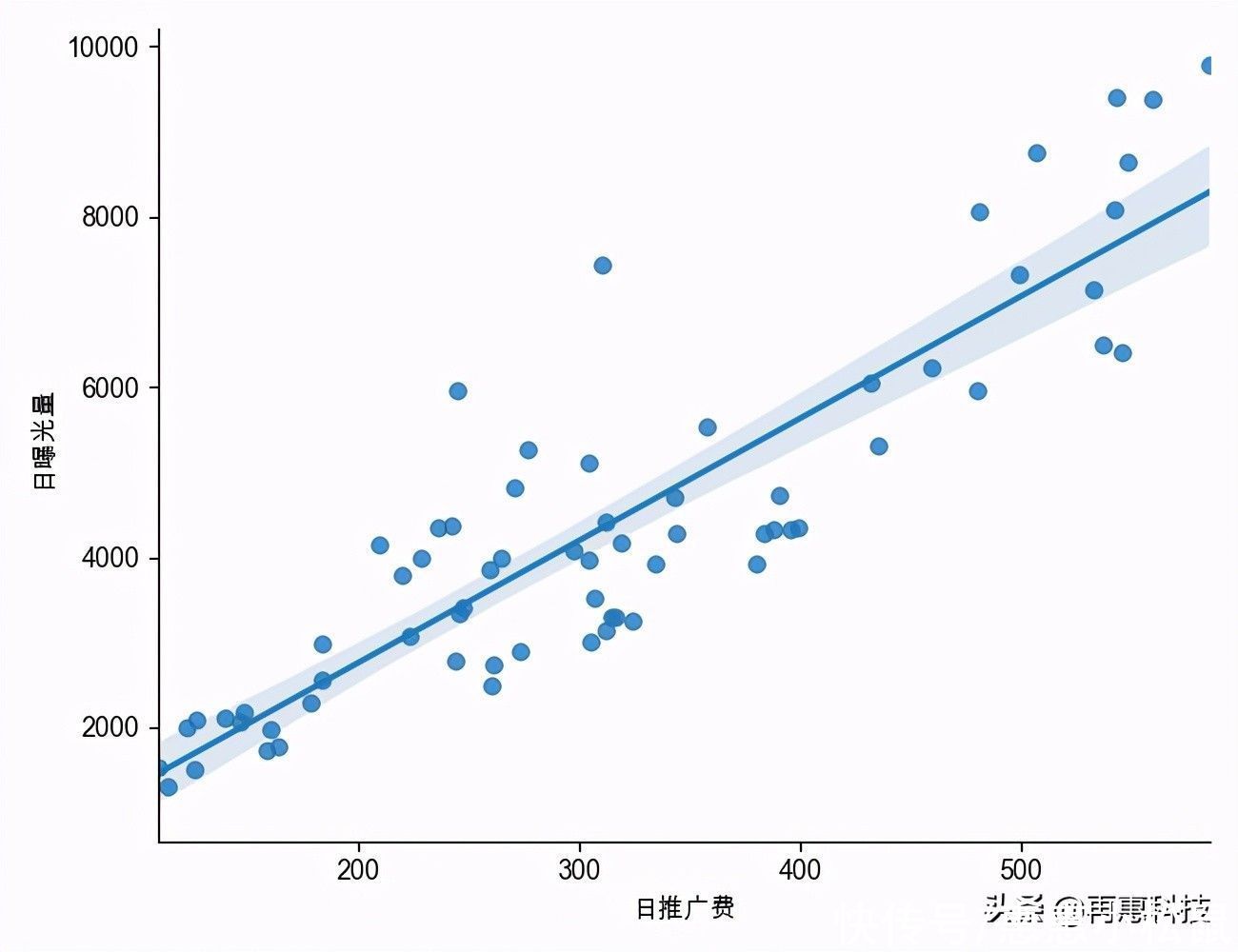
图中的散点：

店铺一天的日推广费对应的日曝光量。

图中的直线：

回归线/拟合线，最准确地贯穿图中各点(日曝光量)平均值的直线y=a+bx+e，x为日推广费自变量，y为日曝光量因变量。

计算参数a与b的公式如下：

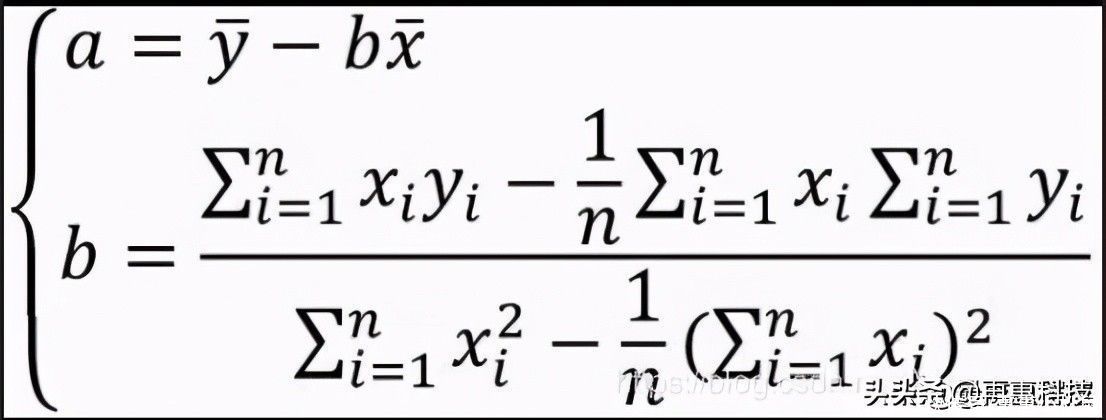
得到拟合线方程y=14.34x-111.13，上面仅近3个月每天的数据，其中最小的日推广费为109.45元/天，即此拟合线方程是在日推广费在109.45~585.48的范围内推算出来的。

一般情况下，数据量越多，范围越广，推算出来的结果效果越好。

以上操作在excel中也可以完成，具体做法如下：

1、选中每天的数据，点击菜单栏“插入”->“图表”->“散点图” 生成图表；

2、在图表上右键“添加趋势线”，趋势线选项中选择“线性”；

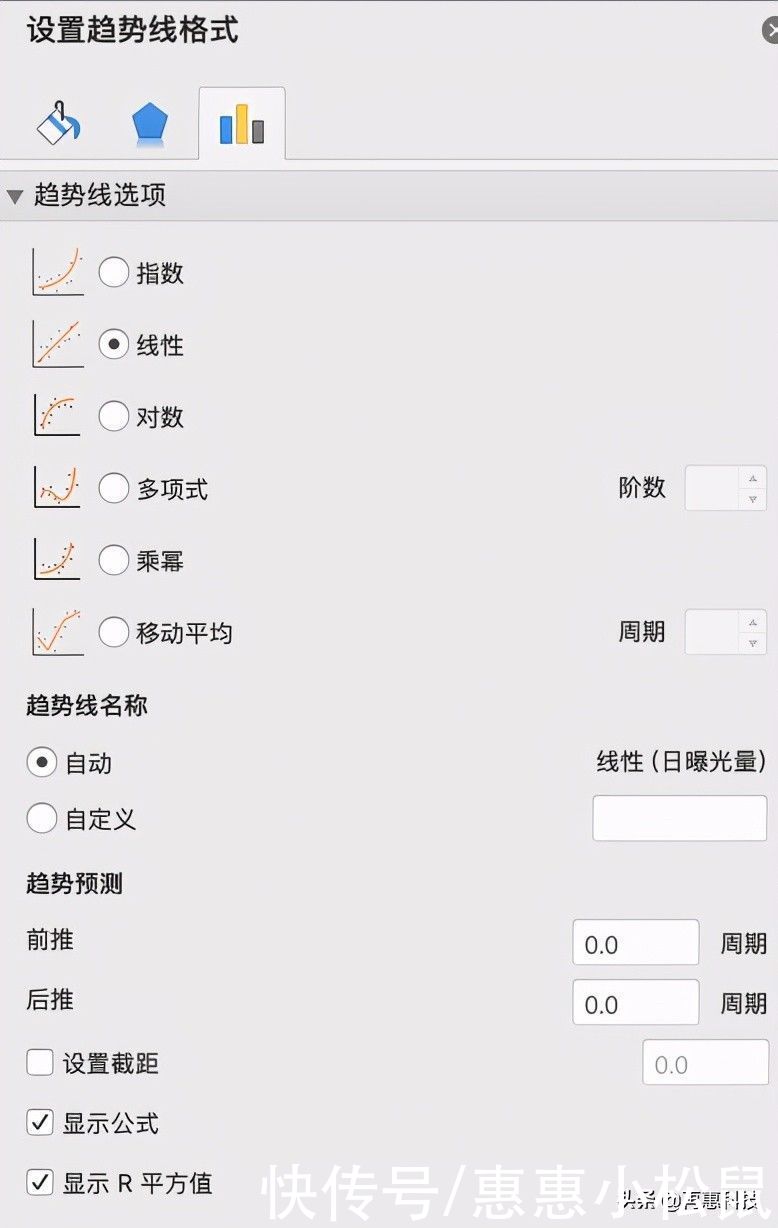
3、趋势预测中勾选“在图表上显示公式”

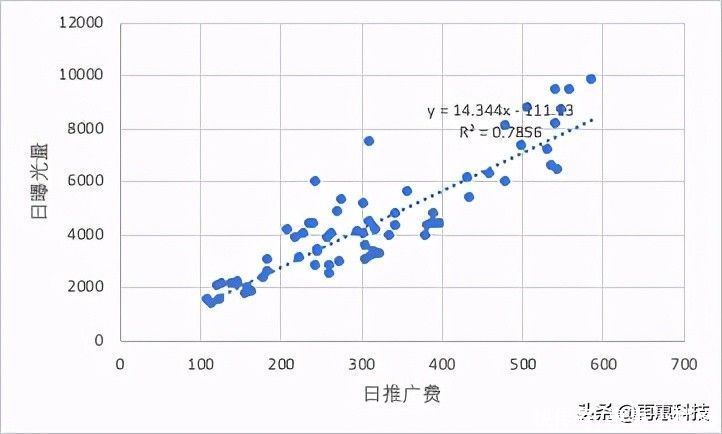
这样，我们可以根据拟合方程来科学的预测日推广费与日曝光量。

例如某店铺想要达到1.5万的日曝光，预计需要投入1053元/天的日推广费；若店铺日推广费最多预算为800元，那预计会带来11360的曝光量，再根据店铺的转化率等，即可大致推算出下单量与营业额。

每当散点图有较好线性关系的时候，就可以尝试用这种预测方法来进行预测。